Как сделать из задачи уравнение

Решение задачи обычно включает рациональное рассуждение и расчеты для нахождения значения величины. Например, нахождение количества скорости, времени, расстояния, массы объекта или чего-то еще.

Такие задачи можно решить с помощью уравнений. Это предполагает размещение переменных перед искомым значением, а затем использование рациональных рассуждений, структуры уравнения и решения. После решения уравнения проводится проверка, удовлетворяет ли решение уравнения условиям задачи.

Запись выражений, содержащих неизвестное

Решение задачи сопровождается уравнением задачи. Начальным этапом решения учебной задачи должно стать обучение созданию алфавитного представления, описывающего ту или иную жизненную ситуацию. Этот этап не является сложным и может быть изучен в процессе решения проблемы.

Рассмотрите различные ситуации, которые можно записать с помощью математических выражений.

Работа 1. Отцу X лет. Мать на два года моложе. Сын в три раза моложе отца. Запишите возраст каждого человека, используя выражение.

Решение.

Задача 2. Отцу X лет, а мать на 2 года моложе отца. Сын в три раза моложе отца, а дочь в три раза моложе матери. Напишите возраст каждого человека, используя выражение.

Решение.

Вопрос 3. Отцу X лет, а мать на три года моложе отца. Сын в три раза моложе отца, а дочь в три раза моложе матери. Если общий возраст отца, матери, сына и дочери составляет 92 года, то сколько лет всем?

Решение.

В этой задаче, помимо записи представительства, необходимо рассчитать возраст каждого члена семьи.

Сначала запишите возраст каждого члена семьи, используя выражение. Возьмите возраст отца в качестве переменной X, а затем используйте эту переменную для создания других выражений.

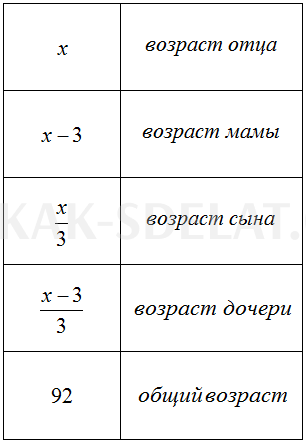
Теперь определите возраст всех членов семьи. Для этого необходимо составить и решить уравнение. Все элементы уравнения готовы. Остается только собрать их.

Общий возраст 92 года складывается из дополнительных возрастов отца, матери, сына и дочери.

С каждым возрастом мы создавали математические выражения. Эти выражения являются компонентами уравнения. Для составления уравнений следуйте приведенной выше схеме и таблице. Другими словами, замените слова отец, мать, сын и дочь соответствующими им выражениями в таблице.

Выражение, соответствующее возрасту мамы x -3, для наглядности помещено в скобки.

Теперь решим полученное уравнение. Первоначально откройте скобки как можно дальше.

Чтобы ослабить уравнение от дробей, умножьте обе части на 3

Решите полученное уравнение, используя известные преобразования тождеств.

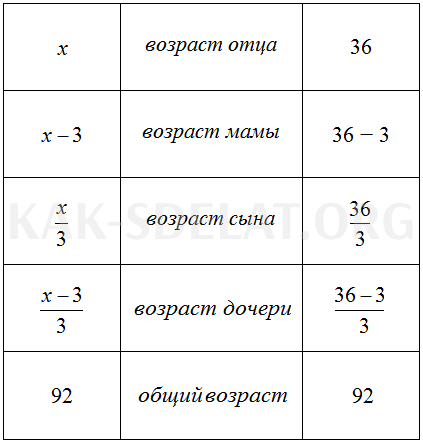
Значение для переменной x найдено. Эта переменная отвечала за возраст отца. Таким образом, возраст отца составляет 36 лет.

Зная возраст отца, вы можете рассчитать возраст остальных членов семьи. Для этого замените значение переменной X в выражении, отвечающем за возраст конкретного члена семьи.

В задаче говорится, что мать на три года моложе отца. Мы указываем ее возраст, выражая х-3. Поскольку значение X теперь известно, мы подставляем значение 36 вместо X в выражение X -3 для расчета возраста МОМ.

X -3 = 36-3 = 33 года для мамы.

Возраст других членов семьи определяется таким же образом.

Чек:.

Вопрос 4. Килограмм яблок стоит х рублей. Напишите уравнение для вычисления количества яблок, которые можно купить за 300 рублей.

Решение.

Если килограмм яблок стоит х рублей, вы можете купить килограмм яблок за 300 рублей.

Пример Килограмм яблок стоит 50 рублей. Впоследствии покупается 300 рублей, то есть 6 кг яблок.

Вопрос 5. За X рублей было куплено 5 кг яблок. Напишите уравнение для расчета стоимости килограмма яблок.

Решение.

Если за 5 кг платят X рублей, то килограмм яблок стоит X рублей.

Пример За 300 рублей было куплено 5 кг яблок. Тогда килограмм яблок будет стоить. Другими словами, она стоит 60 рублей.

Вопрос 6. Том, Джон и Лео идут в столовую во время перерыва и покупают сэндвич и кофе. Бутерброд стоит x рублей, а кружка для кофе — 15 рублей. Определите стоимость бутерброда, если известно, что за все было заплачено 120 рублей?

Решение.

Конечно, проблема проста, как девочка, и ее можно решить, не прибегая к уравнениям. Для этого отнимите стоимость 3 чашек кофе от 12 рублей (15 х 3) и разделите полученный результат на 3.

Однако наша цель — составить уравнение для задачи и решить это уравнение. Таким образом, стоимость бутерброда составляет X рублей. Только три из них были куплены. Таким образом, увеличение цены в три раза дает выражение, описывающее количество рублей, заплаченных за три бутерброда.

3x- стоимость трех сэндвичей

Затем мы можем записать стоимость трех чашек кофе в виде 15×3. 15 — это цена чашки кофе, а 3 — множитель, который увеличивает цену в три раза (Том, Джон и Лео).

Согласно условиям задачи, за все будет выплачено 120 рублей. У нас уже есть примерный план, что делать:.

У нас уже есть выражения, описывающие стоимость трех бутербродов и трех чашек кофе. Это уравнения 3 x и 15 x 3. Используйте схему для составления и решения уравнений.

Таким образом, стоимость сэндвича составляет 25 рублей.

Задача может быть решена только в том случае, если уравнения записаны правильно. В отличие от обычных уравнений, где вы учитесь находить корни, уравнения для решения задач имеют свое особое применение. Каждый компонент такого уравнения может быть описан словесно. При составлении уравнения необходимо понимать, зачем вы включаете компоненты и зачем они вам нужны.

Также необходимо помнить, что уравнения равны и что левая часть должна быть равна правой. Составленное уравнение не должно противоречить этой идее.

Представьте, что уравнение — это экран, на котором отображаются две чашки весов и состояние весов.

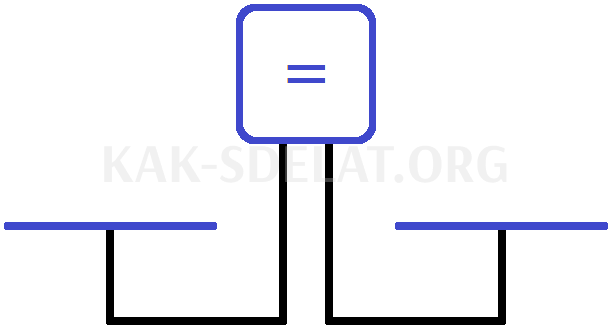
Символы равенства в настоящее время находятся на экране. Чаша слева равна чаше справа, что очевидно. На весах ничего нет. Запишите состояние весов и то, что в чашках нет элементов, используя следующее уравнение

Поместите арбуз на левую чашу весов: .

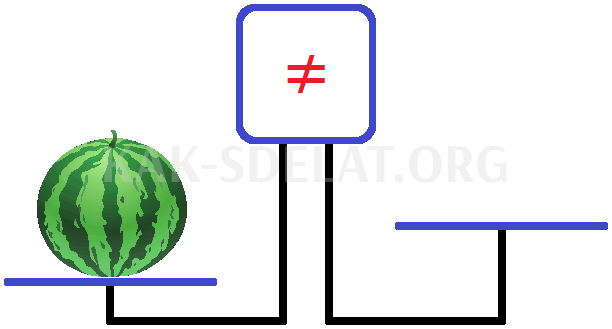
Левая чаша больше правой, и экран подал сигнал тревоги, показав символ неравенства. Этот символ говорит о том, что левая чаша не равна правой.

Теперь давайте попробуем решить эту проблему. Найдите вес арбуза в левой чаше. Но как мы можем научиться этому? Наши весы предназначены только для проверки того, равна ли левая чаша правой.

Уравнение будет похоже на сохранение. Помните, что уравнение по определению является равенством, содержащим переменные, значения которых необходимо найти. В данном случае гири играют роль в этом уравнении, а масса арбуза является переменной, значение которой необходимо найти. Наша цель — найти правильное уравнение. Поймите масштаб, чтобы вы могли рассчитать массу арбуза.

Для соответствия масштабу более тяжелые предметы можно поместить на соответствующую шкалу. Например, поставьте вес 7 кг.

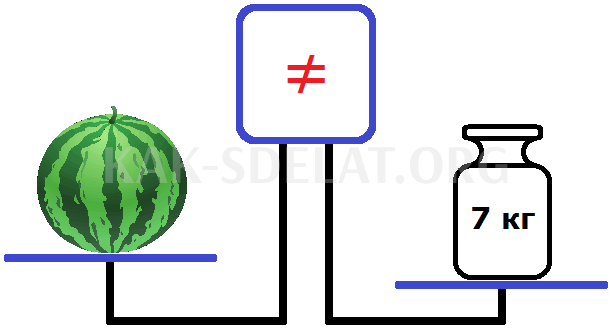
Сейчас действует обратное. Миска справа лучше, чем миска слева. На экране по-прежнему отображается, что чашки не равны.

Положим в левую чашу гирю весом 4 кг.

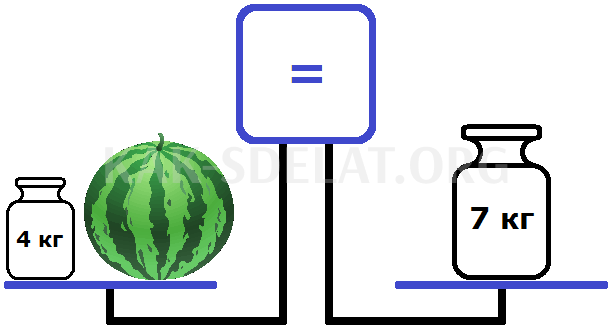
Теперь грузы будут находиться на одном уровне. На рисунке видно, что левая чаша имеет ту же высоту, что и правая. Затем на экране появится знак равенства. Этот знак показывает, что левая чаша равна правой.

Следовательно, существует уравнение — равенство с неизвестными. Левая чаша является левой частью уравнения и состоит из компонента 4 и переменной x (масса арбуза), а правая чаша является правой частью уравнения и состоит из компонента 7.

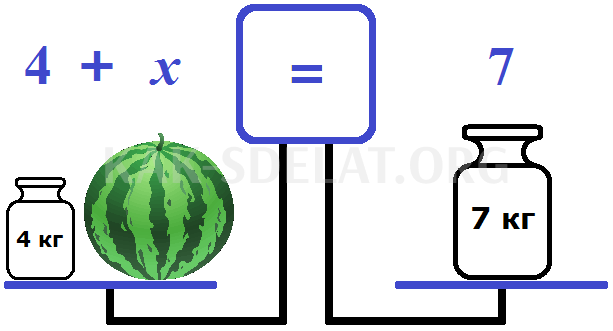
Теперь нетрудно вывести, что корень уравнения 4 + x = 7 равен 3. Таким образом, масса арбуза равна 3 кг.

То же самое относится и к другим проблемам. Чтобы найти неизвестные значения, к левой или правой части уравнения добавляются различные элементы, такие как суммы, множители и выражения. В школьных задачах эти элементы уже даны. Остается только правильно их структурировать и построить уравнение. В этом примере для расчета массы арбуза были использованы различные гири.

Конечно, данные, приведенные в задаче, должны быть сначала приведены к форме, которая может быть включена в уравнение. Так что, как говорится, "стоит задуматься".

Рассмотрим следующую проблему. Возраст отца равен суммарному возрасту его сына и дочери. Сын вдвое старше дочери и на 20 лет моложе отца. Сколько им всем лет?

Возраст дочери можно выразить как x. Если сын в два раза старше дочери, его возраст обозначается 2x. В рассматриваемых условиях возраст дочери и сына вместе равен возрасту отца. Таким образом, возраст отца представлен суммой x+2x.

Аналогичные суммы можно добавить к уравнению. Возраст отца обозначается через 3x

Теперь создадим уравнение. Нам нужно получить уравнение, в котором мы сможем найти неизвестное x Используйте гири. Введите возраст отца (3 x) слева и возраст сына (2 x) справа.

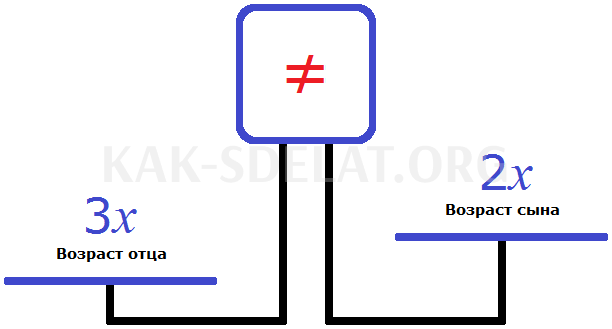
Вы увидите, почему левая чаша превышает правую и почему на экране появляется символ (!=). Естественно, что возраст отца старше возраста сына.

Однако для вычисления неизвестного x весы должны быть уравновешены. Для этого необходимо добавить числа к соответствующему масштабу. Какое именно число упоминается в вопросе? Согласно ситуации, сын на 20 лет моложе отца. Поэтому 20 лет — это то число, которое мы должны положить на чашу весов.

Добавление 20 лет к правой стороне шкалы уравновешивает ее. Другими словами, мы доводим сына до возраста его отца.

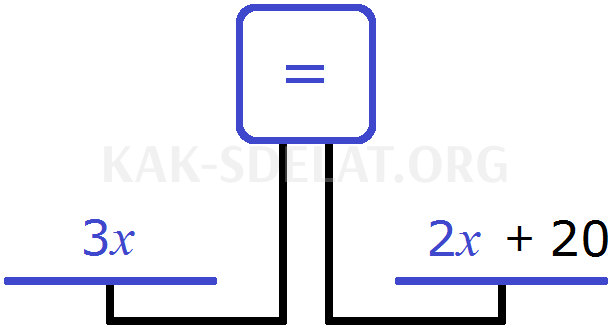
Теперь шкала выровнена. Уравнение оказывается легко решаемым.

Первым шагом в решении этой задачи было объявление возраста дочери с помощью переменной x. Теперь мы нашли значение этой переменной. Дочери 20 лет.

Затем нам сказали, что сын на два года старше дочери, поэтому сыну (20 x 2), т.е. 40 лет.

Наконец, рассчитайте возраст отца. В вопросе сказано, что она равна сумме возрастов сына и дочери, т.е. (20 + 40).

Давайте вернемся к сути проблемы и обратим внимание на одну вещь. Если мы посмотрим на возраст отца и возраст сына на шкале, то шкала слева будет больше, чем шкала справа.

Однако добавление еще 20 лет к правильной шкале решает проблему. В результате весы теперь уравновешены и равны.

Однако вместо того, чтобы добавить эти 20 лет к правой шкале, можно было вычесть их из левой шкалы. И в этом случае мы получим уравнение

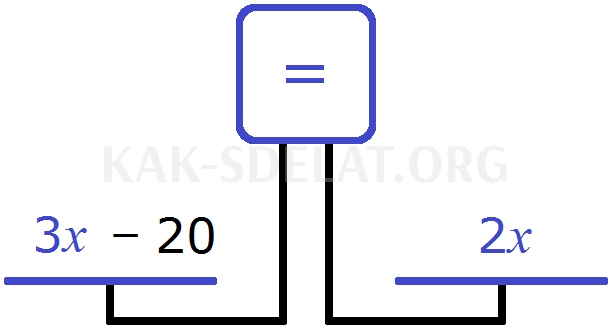
На этот раз у нас есть уравнение. Корень уравнения по-прежнему равен 20.

Другими словами, уравнения эквивалентны. И помните, что уравнения имеют одинаковые корни. Если мы внимательно рассмотрим эти два уравнения, то увидим, что второе уравнение является результатом переноса числа 20 из правой части в левую часть с противоположным знаком. И, как уже говорилось в предыдущем уроке, это действие не изменяет корни уравнения.

Также обратите внимание, что в начале задачи возраст каждого члена семьи может быть задан другими выражениями.

Предположим, что возраст сына представлен через x, а возраст дочери через , поскольку она вдвое старше дочери (что в два раза меньше возраста сына). Возраст отца представлен через , так как это сумма возрастов сына и дочери. И, наконец, чтобы составить логически правильное уравнение, прибавьте 20 к возрасту сына, потому что отцу 20 лет. В результате получается совершенно другое уравнение. Давайте решим это уравнение.

Как видите, ответ на проблему не изменился. Сыну еще 40 лет. Дочери еще нет 40 лет, а отцу уже за 40.

Другими словами, проблемы можно решать разными способами. Поэтому не отчаивайтесь, если вы не можете решить какую-то конкретную проблему. Однако следует помнить, что существуют и более простые способы решения проблем. До центра города можно добраться разными путями, но всегда есть самый удобный, быстрый и безопасный маршрут.

Примеры решения задач

Задача 1.В двух пачках только 30 тетрадей. Если из первой пачки во вторую переложить две тетради, то в первой пачке будет в два раза больше тетрадей, чем во второй. Сколько тетрадей было включено в каждую упаковку?

Решение.

Обозначьте символом x количество тетрадей, которые были включены в первую упаковку. Если общее количество тетрадей равно 30, а x — количество тетрадей в первой стопке, то количество тетрадей во второй стопке представляется формулой 30-x. То есть, общее количество тетрадей вычитается из количества тетрадей в первой стопке, чтобы получить количество тетрадей во второй стопке.

Кроме того, если две тетради перемещаются из первой стопки во вторую, считается, что первая стопка содержит в два раза больше тетрадей. Теперь давайте удалим две тетради из первой стопки

Добавьте эти две тетради во вторую стопку

Уравнение, из которого нам необходимо вывести уравнение, будет иметь вид

Давайте составим уравнение из имеющегося у нас уравнения. Положим обе стопки тетрадей на весы

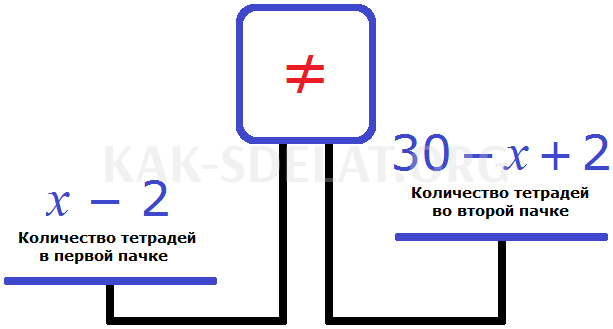
Левая чаша тяжелее правой. Это происходит потому, что, для иллюстрации проблемы, после того, как вы взяли две тетради из первой стопки и положили их во вторую стопку, количество тетрадей в первой стопке в два раза больше количества тетрадей во второй стопке.

Чтобы уравнять масштаб и получить уравнение, удвойте правую часть. Для этого умножьте на 2

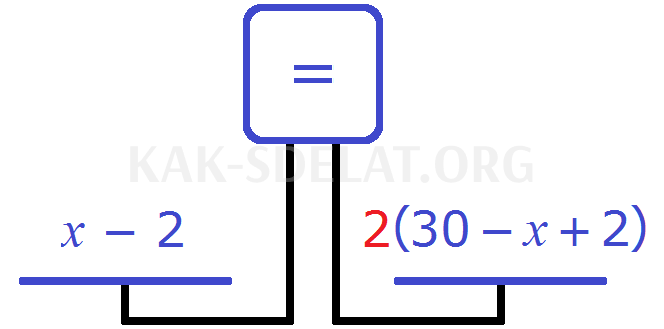
Вы получите уравнение. Давайте решим это уравнение.

Первый стек мы обозначим переменной x. Теперь мы нашли его стоимость. Переменная x равна 22, поэтому в первой стопке было 22 тетради.

Затем мы можем представить вторую пачку уравнением 30 —x, и теперь, когда мы знаем значение переменной x, мы можем вычислить количество квадратов во второй пачке. Это равно 30-22, то есть 8.

Задача 2. Два человека чистили картофель. Один чистил по две картофелины каждую минуту, а другой — по три. Вместе они убрали 400 картофелин. Если вторая операция заняла на 25 минут больше, чем первая, сколько времени длилась каждая операция?

Решение.

Обозначим рабочее время первого человека через x. Второй человек работал на 25 минут дольше, чем первый, поэтому его время показано как

Первый рабочий чистил 2 картофелины в минуту, и когда он работал в течение x минут, он почистил в общей сложности 2 x картофелин.

Второй человек чистил 3 картофелины в минуту, и когда он работал в течение x минут, он почистил в общей сложности 2 x картофелин.

Вместе они убрали 400 картофелин.

Решите уравнение на основе имеющихся данных. Левая часть уравнения — это количество картофеля, которое нужно очистить с каждого человека, а правая часть — общее количество.

В начале решения этой задачи мы указали рабочее время первого человека через переменную x. Теперь мы нашли значение этой переменной. Первый человек работал в течение 65 минут.

Второй человек работал в течение 1 минуты, и поскольку значение переменной x теперь известно, можно рассчитать время работы второго человека. Это 65 + 25, т.е. 90 минут.

Задача из учебника по алгебре Андрея Киселева. Приготовлено 32 кг чайной смеси. 1 кг первого вида стоит 8 рублей 8 рублей, а 1 кг второго вида стоит 6 рублей. 50 центов. При стоимости килограмма смеси (без прибыли и убытков) 7 рублей, было получено по несколько штук каждого сорта. 10 центов?

Решение.

Дадим определение через X. Определим массу первого семени чая. Затем обозначьте через x массу двух сортов чая, включая выражение 32 -x

Стоимость первого высококачественного чая в количестве 1 кг составляет 8 рублей. Умножьте эти восемь рублей на количество первого высококачественного чая и вы найдете стоимость первого высококачественного чая в X фунтов.

Один килограмм чая II класса стоит 6 рублей. 50 центов. Если цена составляет 6 рублей / 50 девушек. 50 x 32 -X, вы найдете второе число X фунтов высококачественного чая стоимостью 32 раза по X фунтов.

Этот термин гласит, что килограмм смеси будет стоить 7 рублей — 10 девушкам. 10 минут. Всего было произведено 32 кг смеси. Умножьте на 7 трений. 32 девочки 10 девочек могут найти стоимость 32 кг смеси.

Уравнение, из которого нам необходимо вывести уравнение, будет иметь вид

Составим уравнение из имеющегося у нас уравнения. Умножим стоимость смеси первого и второго вида чая на левой стороне шкалы на стоимость 32 кг смеси на правой стороне, то есть общую стоимость обоих видов чая. Синтезировано:.

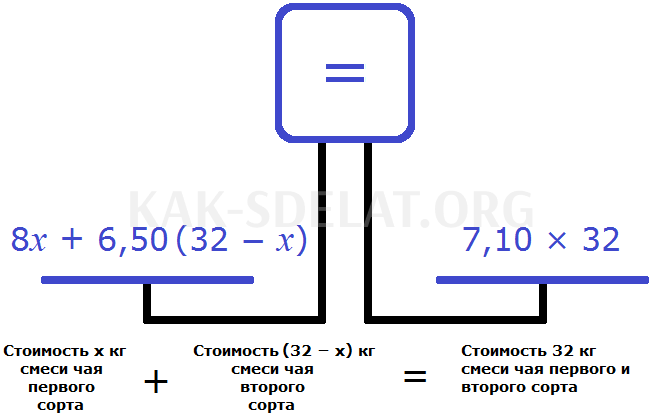
Получите уравнение. Давайте решать:.

В начале решения этой задачи мы указали массу первого сорта чая через переменную x. Теперь мы нашли цену этой переменной. Переменная x равна 12,8. Это означает, что для приготовления смеси было использовано 12,8 кг чая первого сорта.

Уравнение 32 -X можно использовать для выражения массы чая второго сорта, а поскольку значение X теперь известно, можно рассчитать массу чая второго сорта. 32-12.8 IE 19.2. Это означает, что в смеси было использовано 19,2 кг чая второго сорта.

Задача 3. Велосипедист проехал некоторое расстояние со скоростью 8 км/ч. На обратном пути ему пришлось ехать по другой дороге, которая была на 3 км длиннее первой. Насколько большой была дорога?

Решение.

Некоторые проблемы могут быть связаны с вопросами, которые, возможно, не были изучены. Эта проблема — одна из них. Она включает в себя понятия расстояния, скорости и времени. Чтобы решать такие проблемы, необходимо думать о проблеме. В нашем случае нам нужно знать, что такое расстояние, скорость и время.

В нашей задаче нам нужно найти два расстояния. Нам нужно составить уравнения, которые позволят нам вычислить эти расстояния.

Вспомните, как расстояние, скорость и время связаны друг с другом. Каждый из этих размеров может быть учтен в уравнениях знаков.

Используйте правую часть одного из этих уравнений для составления собственного уравнения. Чтобы выяснить, кто из них двоих, обратитесь к тексту, о котором идет речь, и обратите внимание на следующие моменты

Обратите внимание на точку, используемую велосипедистом для дополнительной минуты при возвращении. Это предложение показывает, что вы можете использовать уравнение, т.е. правую часть. Это позволяет нам составить уравнение с переменной s.

Теперь обозначим длину первой дороги. Велосипедист двигался по этому маршруту со скоростью 8 км/ч. Время, затраченное на прохождение этого расстояния, показано в уравнении. Это происходит потому, что расстояние является причиной перехода на эту скорость.

Обратный путь велосипедиста составил 3 км. Поэтому его расстояние выражается как S + 3. Велосипедист ехал по этой дороге со скоростью 9 километров в час. Таким образом, выражается время, необходимое велосипедисту для преодоления расстояния.

Используйте эти уравнения для составления уравнения

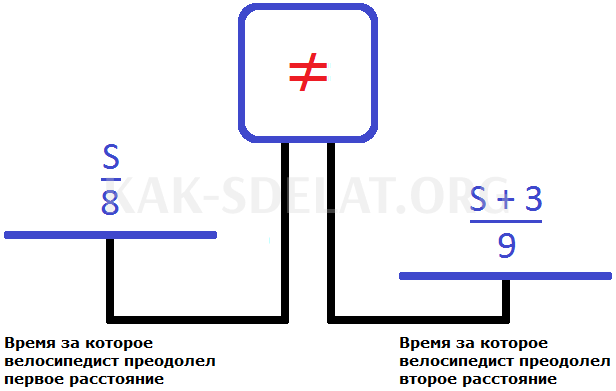
Правая чаша тяжелее левой. Это связано с тем, что проблема указывает на то, что велосипедист потратил больше времени на возвращение домой.

Чтобы уравнять весы, добавьте эти минуты к левой стороне. Однако сначала поменяйте часы на часы, так как проблема измеряется в километрах в час, а не в метрах в час.

Чтобы перевести минуты в часы, нужно разделить их на 60.

Минуты — это часы. Добавьте эти часы к левой части уравнения.

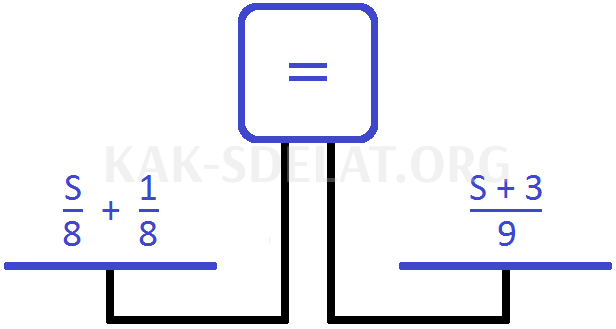
Вы получите уравнение. Решите это уравнение. Чтобы убрать дробь, обе части можно умножить на 72. Затем, используя известное преобразование тождества, найдите значение s

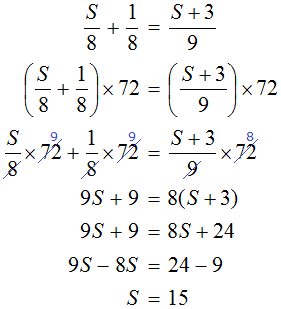
S и объявил расстояние первой дороги. Теперь вы нашли цену этой переменной. Переменная S равна 15. Это означает, что расстояние первой дороги равно 15.

Для второй дороги мы можем использовать формулу S + 3 для вычисления расстояния второй дороги, так как значение переменной S теперь известно. Это равно 15 + 3, т.е. в общей сложности 18 километров.

Задача 4. Два автомобиля движутся по автомагистрали с одинаковой скоростью. Если первый автомобиль увеличит свою скорость на 10 км/ч, а второй уменьшит свою скорость на 10 км/ч, то за 2 часа первый автомобиль преодолеет то же расстояние, что и второй автомобиль за 3 часа. С какой скоростью движется автомобиль?

Решение.

V обозначает скорость каждого автомобиля. Следуя задаче, сделайте несколько предложений: увеличьте скорость первого автомобиля на 10 км/ч и уменьшите скорость второго автомобиля на 10 км/ч. Используйте предложения.

Кроме того, утверждается, что при таких скоростях (увеличивающихся и уменьшающихся на 10 км/ч) первый автомобиль преодолевает то же расстояние за два часа, что и второй за три часа. Фразу "одинаково" можно понимать как "расстояние, пройденное первым автомобилем, равно расстоянию, пройденному вторым автомобилем".

Расстояние, на котором мы помним, определяется средствами массовой информации. Нас интересует правая часть этого буквенного уравнения — мы можем составить уравнение с переменной v.

Таким образом, учитывая скорость v + 10 км/ч, первый автомобиль проезжает 2 (v + 10) км, а второй — 3 (v -10) км. В данной ситуации автомобили проходят одинаковое расстояние, поэтому для составления уравнений достаточно связать эти два уравнения символом равенства. Далее вы получаете уравнение. Решите ее:.

Утверждение в вопросе указывает на то, что автомобили движутся с одинаковой скоростью. Эта скорость символизируется переменной v. Теперь мы нашли цену этой переменной. Переменная v равна 50. Таким образом, скорость обоих автомобилей составила 50 км/ч.

Задача 5. Лодка проходит по реке за 9 часов то же расстояние, что и за 11 часов. Найдите скорость лодки, если скорость течения реки равна 2 км/ч.

Решение.

Выразите собственную скорость судна в терминах v. Скорость течения реки составляет 2 км/ч. Скорость лодки, плывущей по реке, равна v+2 км/ч, а скорость лодки, пересекающей реку, равна (v-2) км/ч.

Согласно описанию задачи, за 9 часов по течению лодка проходит то же расстояние, что и за 11 часов по течению. Выражение "одинаковое расстояние" можно понимать как "расстояние, которое лодка проходит вверх по течению за 9 часов, равно расстоянию, которое она пересекает реку за 11 часов". Другими словами, расстояния будут одинаковыми.

Расстояние определяется уравнением. Используйте правую часть этого буквенного уравнения для составления собственного уравнения.

Таким образом, за 9 часов лодка проходит 9 (v + 2) километров по течению реки, а за 11 часов -11 (v-2) километров против течения реки. Поскольку оба уравнения представляют одно и то же расстояние, приравняем первое уравнение ко второму. В результате получается уравнение. Решите ее:.

Поэтому подходящая скорость для моторной лодки составляет 20 км/ч.

При решении проблемы полезно заранее решить, какой набор решений следует искать.

Предположим, что в задаче требуется найти время, необходимое пешеходу для прохождения заданного пути. Вы представляете время переменной t и составляете уравнение, содержащее эту переменную, чтобы найти ее значение.

Из практики мы знаем, что время движения объекта может принимать целочисленные или дробные значения. 2 часа, 1,5 часа и 0,5 часа. Тогда можно сказать, что для решения задачи требуется набор рациональных чисел Q, поскольку все значения 2, 1,5 и 0,5 часа могут быть выражены в дробной форме.

Поэтому удобно обозначить неизвестную величину переменной, а затем определить множество, к которому она принадлежит. В данном примере время t принадлежит множеству рациональных чисел Q.

Мы также можем ввести ограничение на переменную t и сказать, что она может принимать только положительные значения. На самом деле, если объект прошел определенное количество времени, его время не может быть отрицательным. Поэтому укажем рядом с уравнением t ? Q, что его значение должно быть больше нуля.

Если решение уравнения дает отрицательное значение переменной t, можно сделать вывод, что задача решена неверно, так как решение не удовлетворяет условию t ? Q, t> 0.

Другой пример. Если вы решаете задачу, в которой вам нужно найти количество людей, выполняющих определенную задачу, вы определяете это количество с помощью переменной x. Такая задача ищет решение для множества целых положительных чисел

Действительно, число особей является целым числом, например. 2, 3 или 5. Но не 1,5 (один целый атом и половина атома) или 2,3 (два целых атома и 3/10 атома).

Здесь можно указать, что число атомов должно быть больше нуля, но числа в наборе целых положительных чисел N сами по себе положительны и больше нуля. В этом наборе нет отрицательных чисел и нет нулей. Поэтому выражение x>0 можно опустить.

Операция 6. Для ремонта школы прибыла группа, в которой маляров в 2,5 раза больше, чем плотников. Вскоре Форман добавил в группу еще четырех маляров и перевез двух плотников на другую строительную площадку. В результате в бригаде было в четыре раза больше маляров, чем плотников. Какие маляры и плотники были в бригаде вначале?

Решение.

Обратите внимание на Х плотников, которые первоначально пришли для ремонта.

Количество плотников — это целое число, большее нуля. Следовательно, x принадлежит всем целым положительным числам

Число маляров в 2,5 раза превышало число плотников. Поэтому число художников символизируется как 2,5 раза больше числа маляров.

Кроме того, говорят, что Форман добавил в свою бригаду еще четырех маляров и перевел двух плотников на другие работы. Давайте сделаем то же самое для нашего представительства. Сократите количество плотников на 2 человека

Увеличить количество маляров на 4 человека.

Число плотников и маляров теперь представлено следующим выражением

Давайте составим уравнение из имеющихся выражений.

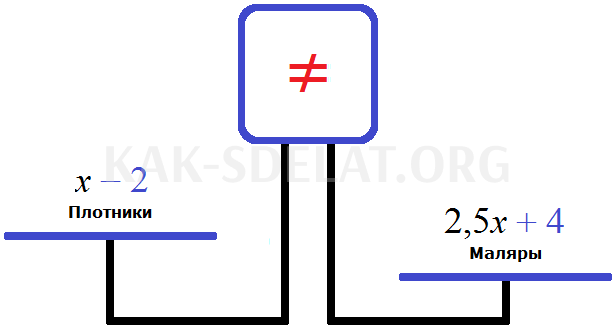
Чаша справа больше. Это происходит потому, что число маляров в группе в четыре раза превышает число плотников, после того как в группу добавляются еще четыре маляра, а два плотника переезжают в разные места. Чтобы выровнять масштаб, левую чашу нужно увеличить в четыре раза.

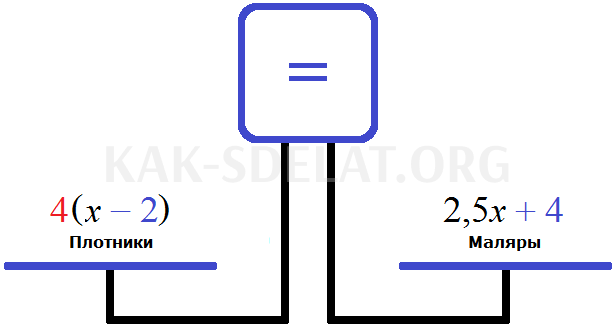
Уравнение дает. Решение.

Мы объявили первоначальное количество плотников с помощью переменной X. Теперь мы нашли цену этой переменной. Поскольку переменная X равна 8, в бригаде изначально было восемь плотников.

Поскольку число маляров равно 2,5 x, а значение переменной x теперь известно, мы можем вычислить число маляров (2,5 x 8, то есть 20).

Возвращаясь к началу задачи, проверяем, что условие x ? N выполнено. Переменная x равна 8, а все элементы положительного целого числа n — это все числа, начинающиеся с 1, 2, 3 и т.д. В этом же наборе найдено число 8.

То же самое можно сказать и о количестве художников. Число 20 принадлежит всем натуральным числам: число 20 принадлежит всем натуральным числам.

Чтобы понять задачу и составить правильное уравнение, вам не нужно использовать масштабную модель с чашками. Можно использовать и другие модели: разделы, таблицы, диаграммы. Вы можете придумать свои собственные модели, которые лучше объясняют природу проблемы.

Работа 9. 30% молока проливается из кувшина. В результате в контейнере остается 14 литров. Сколько литров молока было первоначально в контейнере?

Решение.

Запрашиваемое значение — это исходное количество литров в контейнере. Представим количество литров в виде линии и назовем линию x

Считается, что 30% молока выливается мимо контейнера. Рассмотрим около 30% на диаграмме.

Этот процент, по определению, составляет сантиметр чего-либо. Если 30% молока проливается, остальные 70% остаются в контейнере. Эти 70% соответствуют 14 литрам, упомянутым в вопросе. Назовите оставшиеся 70% на картинке.

Теперь вы можете написать уравнение. Вспомните, как найти процент от числа. Это делается путем деления общего количества вещей на 100 и умножения результата на искомый процент. Обратите внимание, что таким же образом можно получить 14 литров, или 70%. Разделите исходное количество литров x на 100 и умножьте результат на 70.

Или для получения более простого уравнения: запишите 70% в 0,70, умножьте на x и приравняйте полученное уравнение к 14

Таким образом, изначально в контейнере было 20 литров молока.

Вопрос 9. Сфотографированы два сплава золота и серебра. У одного соотношение 1:9, а у другого — 2:3. Сколько каждого сплава необходимо взять, чтобы получить 15 кг нового сплава, в котором золото и серебро находятся в соотношении 1:4?

Решение.

Сначала выясните, сколько золота и серебра может входить в 15 кг нового сплава. В задаче говорится, что соотношение этих металлов должно быть 1:4, т.е. одна часть сплава должна содержать золото и четыре части серебра. Общее количество сплавов будет 1 + 4 = 5, а масса одной части будет 15:5 = 3 кг.

Определите количество золота, содержащегося в 15 кг сплава. Для этого умножьте 3 кг на количество золотых частей.

Определите, сколько серебра содержится в 15 кг сплава.

Так, сплав массой 15 кг содержит 3 кг золота и 12 кг серебра. Теперь вернитесь к оригинальным сплавам. Используйте каждый из них. Пусть x обозначает массу первого сплава, а 15 -x обозначает массу второго сплава.

Выразите все проценты, приведенные в задаче, в виде процентов и занесите их в следующую таблицу.

В первом сплаве золото и серебро находятся в соотношении 1:9. Тогда общее количество деталей будет 1 + 9 = 10. Золото становится серебром.

Перенесите данные в таблицу. Давайте представим 10% на передовой в области "Золотая ставка сплава". Введите 90% в передней части поля "Процент серебра в сплаве". В последнем столбце "Масса сплава" запишите переменную X, так как это масса первого сплава.

Сделайте то же самое для второго сплава. Соотношение золота и серебра составляет 2:3. В этом случае общее количество деталей равно 2 + 3 = 5. Для золота, серебра это так.

Перенесите эти данные в таблицу. Запишите 40% во второй колонке столбца "Золотая норма сплавов" и 60% во второй колонке столбца "Серебряная норма сплавов". 60% во второй колонке столбца "Коэффициент серебрения сплавов". Затем напишите 15 — x в последней строке столбца "Масса сплава", потому что вы написали массу второго сплава.

Завершите последний ряд. Полученный сплав массой 15 кг содержит 3 кг золота, которое является сплавом, и серебро — сплав. В последнем столбце напишите массу полученного сплава15.

Теперь вы можете использовать эту таблицу для составления уравнения. Напомните себе о проблемах концентрации, сплавов и смесей. Если сложить золото обоих сплавов по отдельности и сделать эту сумму равной массе получившегося золота сплавов, то можно найти значение X.

Кроме того, для удобства ставки выражены в виде дробных долей.

В первом сплаве содержание золота составляло 0,10 x, а во втором сплаве — 0,40 (15 — x). Масса золота в полученном сплаве равна сумме масс золота в первом и втором сплавах, что составляет 20% от массы нового сплава. Также 20% нового сплава составляют ранее рассчитанные 3 кг золота. Следовательно, имеем уравнение 0,10 x + 0,40 (15 — x) = 3. Решите это уравнение.

Первоначально через X обозначается масса первого сплава. Теперь мы нашли цену этой переменной. Переменная x равна 10, символизируя массу второго сплава через 15 -x. Поскольку мы знаем значение переменной x, мы можем вычислить массу второго сплава: 15 — 10 = 5 кг. Масса второго сплава может быть рассчитана по переменной x.

Это означает, что мы получаем 5 кг из второго сплава, чтобы получить новый сплав массой 15 кг, где золото и серебро поступают из первого сплава 1:4, 10 кг.

Уравнение также можно выполнить, используя вторую колонку таблицы результатов. Тогда есть уравнение 0,90 x + 0,60 (15 — x) = 12. Корень этого уравнения также равен 10

Задача 10. Имеются руды двух месторождений с содержанием меди 6% и 11%. Какое количество бедной руды необходимо проглотить, чтобы получить 20 тонн 8% меди при смешивании с богатой рудой?

Решение.

Пусть x обозначает массу бедной руды. Поскольку необходимо взять 20 тонн руды, это означает, что из богатой руды берется 20-x. Содержание меди в бедной руде составляет 6%, поэтому x тонн руды будет содержать 0,06x тонн меди. Богатая руда содержит 11% меди, что означает, что 20 x тонн богатой руды содержат 0,11 (20-x) тонн меди.

Полученные 20 тонн руды должны содержать 8% меди. Поэтому 20 тонн руды будут содержать 20 x 0,08 = 1,6 тонны меди.

Добавьте 0,06 x и 0,11 (20-x), чтобы получить в сумме 1,6. Получаем уравнение 0,06x+ 0,11 (20-x) = 1,6

Решите это уравнение.

Таким образом, для получения 20 тонн руды с содержанием меди 8% необходимо получить 12 тонн бедной руды. Тем не менее, получено 20-12 = 8 тонн богатой руды.

Вопрос 11: После увеличения средней скорости с 250 до 300 м/мин спортсмен начинает пробегать дистанцию на 1 минуту быстрее. Какова продолжительность курса?

Решение.

Длина дистанции (или расстояние дистанции) может быть выражена в буквах с помощью следующего уравнения.

Используйте правую часть этого уравнения для составления уравнения. Вначале спортсмен пробежал дистанцию со скоростью 250 метров в минуту. При этой скорости длина пути представлена уравнением 250t.

Затем спортсмен увеличил скорость до 300 метров в минуту. При этой скорости длина пути представлена уравнением 300t.

Обратите внимание, что длина пути постоянна. Независимо от того, увеличивает или уменьшает спортсмен свою скорость, длина дистанции остается неизменной.

Это позволяет сделать 250 т и 300 т равными. Это связано с тем, что они оба представляют одно и то же расстояние.

Однако из задачи следует, что при скорости 300 метров в минуту он пробежал дистанцию на одну минуту быстрее. Другими словами, при скорости 300 метров в минуту время работы сокращается на единицу. Таким образом, уравнение 250 t = 300 t уменьшает время в правой части на единицу.

Это простое уравнение. Давайте решим эту проблему:.

При скорости 250 метров в минуту спортсмен преодолевает дистанцию за 6 минут. Зная скорость и время, можно определить длину дистанции.

S = 250 x 6 = 1500 метров.

А при заданной скорости 300 метров в минуту спортсмен может преодолеть дистанцию за t-1, то есть за 5 минут. Как уже упоминалось выше, продолжительность курса остается неизменной.

S = 300 x 5 = 1500 м

Вопрос 12: Велосипедист обгоняет пешехода на расстоянии 15 км. Если первый движется со скоростью 10 км в час, а второй только 4 км в час, то через сколько часов велосипедист доберется до пешехода?

Решение.

Проблема заключается в мобильности. Это можно решить, определив скорость сближения и разделив начальное расстояние между велосипедистом и пешеходом на эту скорость.

Скорость сближения определяется путем вычитания минимальной скорости из максимальной.

10 км/час — 4 км/час = 6 км/час (скорость приближения)

Расстояние в 15 км сокращается на 6 км каждый час. Чтобы найти момент, когда она полностью сокращается (когда велосипедист достигает пешехода), разделите 15 на 6.

2,5 часа — это 2,5 часа. А 30 минут — это 30 минут. Таким образом, велосипедист достигает пешехода за 2 часа 30 минут.

Решите эту задачу с помощью уравнения.

Предположим, что пешеход и велосипедист стартуют из одной и той же точки. Пешеход покидает всадника и проходит 15 км.

Затем велосипедист последовал за ним по дороге со скоростью 10 км/ч. Скорость пешехода составляет 4 км/ч. Это означает, что через некоторое время велосипедист догоняет пешехода. Мы должны найти это время.

Когда велосипедист догоняет пешехода, это означает, что они вместе проехали одинаковое расстояние. Расстояние, пройденное велосипедистом и пешеходом, представлено следующим уравнением

Используйте правую часть этого уравнения для составления собственного уравнения.

Расстояние, пройденное велосипедистом, представлено уравнением 10t. Пешеход начал маршрут раньше всадника и успел проехать 15 км, поэтому пройденное расстояние представлено уравнением 4 t+15.

К тому времени, когда велосипедист догнал пешехода, они оба проехали одинаковое расстояние. Это позволяет сделать расстояние, пройденное велосипедистом и пешеходом, одинаковым.

Это простое уравнение. Давайте решим эту проблему:.

Задачи для самостоятельного решения

Задача 1. Пассажирский поезд прибывает из одного города в другой на 45 минут быстрее, чем коммерческий поезд. Если скорость пассажирского поезда 48 км/ч, а скорость товарного поезда 36 км/ч, найдите расстояние между городами.

Решение.

Скорость поезда в этой задаче измеряется в километрах в час. Поэтому переведите 45 минут, указанные в задаче, в часы. 45 минут — это 0,75 часа.

Время, которое требуется товарному поезду, чтобы добраться до города, представлено переменной t. Пассажирский поезд прибывает в город на 0,75 часа раньше, поэтому его время работы равно t-0,75.

Пассажирский поезд проехал 48 (t-0,75) км, а коммерческий — 36 т км. Поскольку мы говорим об одном и том же расстоянии, давайте приравняем первое уравнение ко второму. Полученное уравнение равно 48(t-0,75) = 36t. Решение:.

Далее рассчитаем расстояния между городами. Для этого умножим скорость товарного поезда (36 км/ч) на время в пути t. Теперь мы знаем, что значение t равно 3 часам.

Скорость пассажирского поезда также может быть использована для расчета расстояния. Однако в этом случае значение t должно быть уменьшено на 0,75, поскольку пассажирский поезд проходит путь на 0,75 часа меньше.

48 x (3-0,75) = 144-36 = 108 км

ОТВЕТ: расстояние между городами составляет 108 км.

Вопрос 2.Два автомобиля выезжают из города на расстояние 150 км и сталкиваются друг с другом в одно и то же время. Скорость одного автомобиля была 65 км/ч, а скорость второго — 60 км/ч. Через сколько часов они встретились?

Решение.

Пусть t — это время, необходимое для встречи автомобилей. Во время встречи первый автомобиль проехал 65 т км, а второй — 60 т км. Эти расстояния складываются вместе и равны 150. Получено уравнение 65 t + 60 t = 150.

Значение t равно 1,2. Это означает, что они встретились через 1,2 часа.

ОТВЕТ: машины встретились через 1,2 часа.

Вопрос 3: В трех лабораториях одного завода работает в общей сложности 685 человек. Во второй лаборатории работает в три раза больше работников, чем в первой, а в третьей — в 15 раз больше, чем во второй. Сколько рабочих было в каждом цехе?

Решение.

Пусть x — это работники первой лаборатории. Поскольку во втором цехе было в три раза больше рабочих, чем в первом, мы можем узнать количество рабочих во втором цехе, выразив 3 x. В третьей лаборатории работало на 15 человек меньше, чем во второй. Поэтому количество работников в третьей лаборатории можно выразить уравнением 3x-15.

Задача показывает, что всего было 685 работников. Поэтому сложите x, 3 x и 3 x-15, чтобы в сумме получилось 685. Результат: x + 3 x + (3 x-15) = 685.

Переменная X использовалась для представления количества сотрудников в первой лаборатории. Здесь найдена цена этой переменной — 100 сотрудников. Таким образом, в первой лаборатории работало 100 человек.

Во второй лаборатории было 3 работника, поэтому 3 x 100 = 300, а в третьей лаборатории было 3 x -15, т.е. 3 x 100-15 = 285.

ОТВЕТ: в первом цехе, втором 300 и третьем 285 было 100 рабочих.

Вопрос 4. Две мастерские должны отремонтировать 18 двигателей в течение одной недели в соответствии с планом. Первый цех выполнил план на 120%, а второй — на 125%, таким образом, в неделю ремонтировалось 22 двигателя. Каков был план ремонта двигателя на одну неделю в каждой лаборатории?

Решение.

Приводы X ремонтируются в первой мастерской. Во втором цехе будут отремонтированы двигатели 18 -X.

Первая мастерская выиграла 120% от своего плана, что означает, что он отремонтировал двигатель 1.2 X. А вторая мастерская выиграла 125% от своего плана, что означает, что он отремонтировал 1,25 (18 -x) двигателей.

В выпуске сообщается, что было отремонтировано 22 двигателя. Поэтому можно сложить 1,2 x и 1,25 (18 -x) и тогда общая сумма будет равна 22. В результате получается уравнение 1,2 x + 1,25 (18 -x) = 22.

Переменная x использовалась для определения количества двигателей, которые необходимо было отремонтировать в первой мастерской. Теперь мы нашли значение этой переменной, которое составляет 10 лет. Поэтому в первой мастерской необходимо было отремонтировать 10 двигателей.

Уравнение 18 -x представляет собой количество двигателей, подлежащих ремонту во второй мастерской. Следовательно, во второй мастерской нужно было отремонтировать 18 — 10 = 8 двигателей.

ОТВЕТ: 10 двигателей нужно было отремонтировать в первой мастерской и 8 двигателей нужно было отремонтировать во второй мастерской.

Вопрос 5: Цена на товар выросла на 30% и теперь стоит 91 руб. Какова была стоимость товара до повышения цены?

Решение.

Предположим, что до повышения цены стоимость продукта составляла x рублей. Если цена увеличилась на 30%, это означает, что цена увеличилась на 0,30 х руб. После повышения цены стоимость продукта стала составлять 91 рубль. Добавьте x к 0,30 x и приравняйте эту сумму к 91. Результат: x + 0,30 x = 91.

Это означает, что стоимость продукта будет стоить 70 рублей до повышения цены.

ОТВЕТ: стоимость товара до повышения цены составляет 70 рублей.

Вопрос 6.Число увеличилось на 25%. На сколько будет уменьшаться новое число, пока не достигнет первоначального?

Решение.

Пусть x — исходное число. Увеличьте его на 25%. Вы получаете формулу x + 0,25 x. Рассмотрим аналогичную сумму и получим x + 0,25 x = 1,25 x.

Выясните, какая часть исходного числа x содержится в новом числе 1,25 x

Если новое число 1,25 x равно 100%, а исходное x равно 80%, уменьшите новое число на 20%, чтобы получить исходное число x

ОТВЕТ: чтобы получить исходное число, новое число нужно уменьшить на 20%.

Решение.

Пусть x — исходное число. Увеличьте его на 20%. Вы получаете выражение x + 0,20 x. Приравняйте эту сумму к 144 и получите выражение x + 0,20 x = 144

ОТВЕТ: исходное число — 120.

Решение.

Пусть x — исходное число. Уменьшить на 10%. Таким образом, вы получите выражение x -0,10 x. Приравняем эту разность к 45, поэтому выражение x -0,10 x = 45

ОТВЕТ: первоначальное значение числа равно 50.

Вопрос 9: Цена альбома сначала снижается на 15%, затем еще на 15 рублей. Новая цена альбома после двух сокращений составила 19 рублей. Указана первоначальная цена альбома.

Решение.

Пусть x — это первоначальная цена альбома. Уменьшите это значение на 15% и получите x -0,15 x. Уменьшим цену еще больше — до 15 рублей, тогда мы имеем x -0,15 x -15. После снижения цены стоимость альбома теперь составляет 19 рублей. Приравнивая выражение x -0,15 x -15 к равному x -19, получим выражение x -0,15 x -15 = 19

ОТВЕТ: первоначальная цена альбома составляет 40 рублей.

Вопрос 10: При высушивании травы теряется 80% ее массы. Сколько тонн травы необходимо скосить, чтобы получить 4 тонны сена?

Решение.

Если 80% массы теряется, то оставшиеся 20% дают 4 тонны соломы. Из X тонн травы должно получиться 4 т сена. Если 4 т соответствует 20% травы, можно составить уравнение.

ОТВЕТ: чтобы заготовить 4 т сена, нужно скосить 20 т травы.

Вопрос 11: Сколько фунтов 20%-ного солевого раствора нужно добавить к 1 кг 10%-ного солевого раствора, чтобы получить 12%-ный солевой раствор?

Решение.

Добавьте XG 20%-ного солевого раствора к 1 кг 10%-ного солевого раствора.

1 кг 10%-ного солевого раствора содержит 0,1 кг соли. x кг 20%-ного солевого раствора содержит 0,20 x кг соли.

После добавления x кг 20%-ного раствора новый раствор содержит 0,12 (1 + x) кг соли. Добавьте 0,1 и 0,20 x, чтобы сумма стала равна 0,12 (1 + x). Полученное уравнение равно 0,1 + 0,20 x = 0,12 (1 + x)

ОТВЕТ: чтобы получить 12% раствор соли, необходимо добавить 0,25 кг 20% к 1 кг 10% раствора.

Вопрос 12.Два раствора в воде имеют концентрацию 20% и 30%. Сколько фунтов каждого раствора нужно смешать в одной емкости, чтобы получить 25 кг 25,2%-ного раствора?

Решение.

Пусть x кг первого решения. Так как необходимо приготовить 25 кг раствора, то массу второго раствора можно выразить через 25 -x.

Первый раствор содержит 0,20x кг соли, а второй — 0,30 (25 -x) кг соли. Содержание соли в полученном растворе составляет 25 x 0,252 = 6,3 кг. Сложите уравнения 0,20x и 0,30 (25 -x), чтобы эта сумма равнялась 6,3. Результатом является уравнение.

Это означает, что первое решение стоит GBP12, а второе решение стоит 25 — 12 = 13 кг.

Ответ: первый раствор должен получить 12 фунтов, а второй 13 фунтов.

Понравился ли вам урок? Присоединяйтесь к новой команде Facebook и начните получать уведомления о новых уроках.

Хотите ли вы поддержать проект? Нажмите на кнопку ниже!

46 thoughts on “Решение задач с помощью уравнений”

Потрясающий новый урок. (Хорошо, что вернулся)) Я обязательно выучу этот урок после работы.