Существование окружности, вписанной в треугольник. Основное свойство биссектрисы угла
Определение 1. Биссектриса угла — это радиус, который делит угол на две равные части.
Теорема 1 (Основные свойства частей угла). Каждая часть угла находится на одинаковом расстоянии от стороны угла (рис. 1).
ДОКАЗАТЕЛЬСТВА Рассмотрим любую точку D в укусе вактора и проведем вертикали DE и DF от D до края угла (рис. 1). Прямоугольные треугольники ADF и ADE равны, так как имеют равные углы DAF и DAE, а подчиненные объявления являются общими. Следовательно.
Необходим для доказательства.
Теорема 2 (обратная теорема теоремы 1). Если точки находятся на одинаковом расстоянии от сторон угла, то он лежит на биссектрисе угла (рис. 2).
Доказательство Рассмотрим любую точку D в углу BAC. Он находится на одинаковом расстоянии от края угла. Проведите перпендикуляры DE и DF из D перпендикулярно к краю угла (рис. 2). Прямоугольные треугольники ADF и ADE равны, так как имеют равные DF и DF, а нижний AD является общим. Следовательно.
Необходим для доказательства.
Определение 2. Окружность называется зарегистрированной под углом, если она является касательной к стороне угла.
Теорема 3. Если окружность зарегистрирована под углом, то расстояние от вершины угла до точки касания окружности со стороной угла равно.
Доказательство Пусть d будет записано под углом BAC, а e и f — это e и f вместе с боковыми линиями (рис. 3).
Прямоугольные треугольники ADF и ADE равны, потому что у них равные кривые DF и DF (лучи окружности — это лучи окружности), а меньший AD — общий. Поэтому.
Необходим для доказательства.
Наблюдение. Теорему 3 можно сформулировать и по-другому: из одной точки в другую части касательных линий, проведенных через окружность, равны.
Определение 3. Биссектриса треугольника — это часть угла треугольника, соединяющая верхнюю часть треугольника с противоположной точкой.
Теорема 4. В каждом треугольнике три биссектрисы пересекаются в одной точке.
Доказательство Рассматриваются два ABCS A и C, символизирующие перекресток (рис. 4).
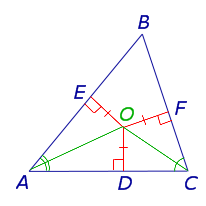
Из O оставьте перпендикуляры OD, OE и стороны треугольника. Так как O лежит на биссектрисе бьющего, равенство справедливо согласно Теореме 1.
Равенство верно, так как точка o лежит на биссектрисе угла ACB согласно Теореме 1.
Следовательно, верно равенство: o — биссектриса угла ACB.
Поэтому из Теоремы 2 следует, что данная точка лежит на биссектрисе угла ABC. Следовательно, все три биссектрисы треугольника проходят через одну точку и должны быть доказаны
Определение 4. Схема регистрации треугольника — это конкретный цикл по всем сторонам треугольника (рис. 5). В этом случае треугольник называется периферийным периферийным треугольником.
Впоследствии. Можно зарегистрировать круг в любом треугольнике, но только в одном. Центр окружности, записанной в треугольнике, — это точка пересечения всех сторон треугольника.
Формулы для радиуса окружности, вписанной в треугольник
Полезно представить типы окружностей, зарегистрированных в треугольниках, в следующей таблице, где указаны радиусы окружностей.
a, b и c — стороны треугольника, s — площадь, r — радиус острия и p — полуокружность.
a — сторона равностороннего треугольника, r — внутренний радиус
где a, b и c — стороны треугольника, s — площадь, r — внутриклеточный радиус и p — полуцикл.
Где a, b и c — стороны треугольника, r — радиус пересечения концов, p — полупинометр.
Где a — сторона равностороннего треугольника, r — радиус в клетке
| Треугольник. |
 |
где a, b и c — стороны треугольника, s — площадь, r — внутриклеточный радиус и p — полуцикл.
Где a, b и c — стороны треугольника, r — радиус пересечения концов, p — полупинометр.
Где a — сторона равностороннего треугольника, r — радиус в клетке
Вывод формул для радиуса окружности, вписанной в треугольник
Теорема 5. Для любого треугольника
где a, b, c — стороны треугольника, r — радиус эндоцитолита, — получувствительный (рис. 6).

Используйте тип герона, который вы получаете:.
Это тоже было проблемой.
Теорема 6. В случае треугольника Исочела применимо следующее равенство
где a — сторона треугольника Изочелла, b — основание и r — радиус цикла регистрации (рис. 7).

Далее, в случае треугольника Изочелла, где
Это тоже было проблемой.
Теорема 7. В случае треугольника Исочела выполняется равенство
где a — сторона треугольника изочелл, а r — радиус в зарегистрированной ячейке (рис. 8).
Тогда в случае равносторонних треугольников
Это тоже было проблемой.
Наблюдение. Читателю предлагается в качестве упражнения извлечь тип луча цикла, который регистрируется непосредственно в равностороннем треугольнике. Другими словами, не используйте общий тип для лучей окружности, зарегистрированных в любом треугольнике или равностороннем треугольнике.
Теорема 8. Для равенства прямоугольных треугольников
Доказательство Рассмотрим рисунок 9.
Четырехугольник CDOF — это прямоугольный треугольник с равными смежными сторонами, поэтому этот четырехугольник является квадратным. Поэтому.
Теорема 3, основанная на уравнении.
Следовательно, учитывая теорему Пифагора, имеем
Это тоже было проблемой.
Наблюдение. Читателю предлагается в качестве упражнения определить тип радиуса окружности, зарегистрированной в прямоугольном треугольнике, через общий тип радиуса окружности, зарегистрированной в любом треугольнике.

 lightanddesign.ru
lightanddesign.ru

















