Деление — это процесс деления целого на равные части. Эта математическая операция полезна не только на уроках математики, но и в повседневной жизни. В этой статье мы расскажем вам, как сделать это самостоятельно. Для этого мы рассмотрим примеры из 3 и 4 классов, где показано деление двузначных и трехзначных чисел.
Класс 3 и 4.
Деление с остатком
Прежде чем перейти к делению последовательностей двух- и трехзначных чисел, важно вспомнить, что подразумевается под "делением с остатком". Проще говоря, это означает деление числа с остатком, который меньше делителя.
Например, разделите 19 на 5. Максимальное число, которое можно разделить от 5 до 19, равно 15. Проверка: 5 x 3 = 15, 19 — 15 = 4. Ответ — 3, остаток — 4. Напишите: 19 : 5 = 3 (4).
Другой пример: разделите 29 на 6. Также найдите наибольшее число, кратное 29 из 6. Ответ равен 24, поэтому остаток равен 4, а остаток равен 5. Запишите 29 : 6 = 4 (5).
Как правильно делить в столбик
Проще делить по столбцам, чем вычислять в уме. Этот метод понятен, обращает внимание на каждый шаг и помогает запомнить алгоритм. Алгоритм работает автоматически.
Деление трехзначного числа на однозначное число
Рассмотрим пример деления трехзначного числа на однозначное через столбец — 322:7. Сначала определим термины.
- 322 — это делитель или то, что делится.
- 7 — делитель или число, на которое нужно разделить.
- Коэффициент — результат действия.
Шаг 1: Поместите делитель 322 слева и делитель 7 справа под углом между ними. Коэффициент измеряется и записывается под делителем.
Шаг 2: Просмотрите делители слева направо и найдите первый неполный делитель. Это значение должно быть больше или равно делителю.
Теперь определите, сколько раз делитель 7 входит в число 32. Разделите на остаток. Разделите 32 на 7. Коэффициент равен 4, а остаток равен 4.
Результат вычитания должен быть меньше делителя. Если нет, то в расчете допущена ошибка. Необходимо увеличить выбранное число и повторно запустить действие.
Шаг 3. Напишите следующую цифру делителя справа от остатка 4. Они говорят "два вниз". Получите следующий делитель 42.
Шаг 4 Сколько раз делитель 7 является делителем числа 42? Кажется, шесть раз. Проверьте: 7 x 6 = 42, 42 = 42 — верно. Запишите 6 в правой четверти — это вторая цифра множителя. Вычтите столбец 42 из 42, остаток равен нулю. Это означает, что числа делятся поровну.
Пример завершает разрешение, и результат равен 46.
Разделите трехзначное число на двузначное, используя пример
Теперь давайте рассмотрим деление трехзначного числа в 3 классе на двузначное число. Примечание: мы перешли к самому сложному.
Пример 1.
Разделим трехзначное число 324 на двузначное число 81.
Шаг 1. В данном случае 324 является кратным числом и должно быть помещено в левый угол. 81 является делителем и должен быть помещен в правую часть.

Шаг 2: Чтобы понять, как разделить двузначное число в столбик, сначала нужно найти число, которое делится на 81. 3 и 32 не совпадают. Оно меньше делителя. Поэтому необходимо найти коэффициент исходного делителя путем подбора. Умножьте столбец 81. Сначала умножьте на 2, потом на 3, потом на 4. 81*4 = 324. совпадение!

Шаг 3: Напишите 4 в столбце под делителем. Вот и ответ.

Пример 2.
Продолжите рассмотрение того, как разделить многозначное число на столбики, на следующем примере. На этот раз разделите 368 на 92.
Шаг 1. Здесь трехзначное число 368 является делителем, а двузначное число 92 — делимым. Поместите их на свои места в колонне.

Шаг 2. Нужно найти наибольший делитель, который можно разделить на 92. 3 и 36 не совпадают, поэтому нужно снова найти делитель. Для этого возьмите десятки и разделите их: 36:9 = 4. Проверьте, совпадают ли эти числа. Умножьте 92 на 4, используя столбцы.

Шаг 4. подходит! Заполните графу коэффициентов в столбце 4.

Как делить однозначные и многозначные числа в столбик с остатком
Как было отмечено в начале, это то же самое деление, за исключением того, что результатом является четное число. Теперь проанализируем тот же пример. Мы просто разделили его на колонки.
Пример 1.
Разделите двузначное число 19 на однозначное число 5. В данном случае 19 — делитель, а 5 — делимое.
Шаг 1. Нарисуйте угол. Поместите делитель 19 слева, а делитель 5 — справа.

Шаг 2. Найдите наибольшее число до 19, которое равномерно делится на 5. Это 15; проверьте, что 5*3=15. Теперь запишите 3 в столбце под делителем и 15 в столбце под делителем.
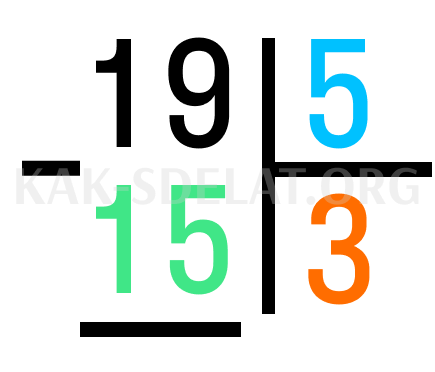
Шаг 3: Вычтите из делителя число, полученное при делении на целое число. 19-15=4. Это остаток.
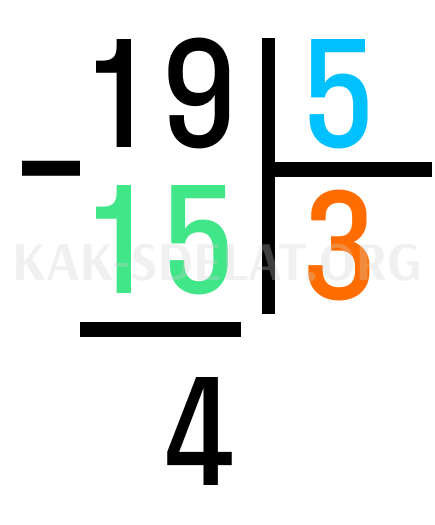
Пример 2.
Разделите двузначное число 29 на однозначное число 6. 29 — делитель, а 6 — делимое.
Шаг 1. Расположите число в столбик. Как обычно, поместите 29 вместо делителя справа от угла, а делитель 6 — слева.

Шаг 2.Найдите число до 29, кратное 2. Проверьте, подходит ли 24: 6 * 4 = 24. Напишите 24 под кратным 29 и 4 в пустом отделении в нижней части угла. Это целочисленная часть, полученная в результате деления.

Шаг 3. Из делителя 29 вычтите число, полученное на шаге 2: 29-24=5. Это оставшаяся часть деления.
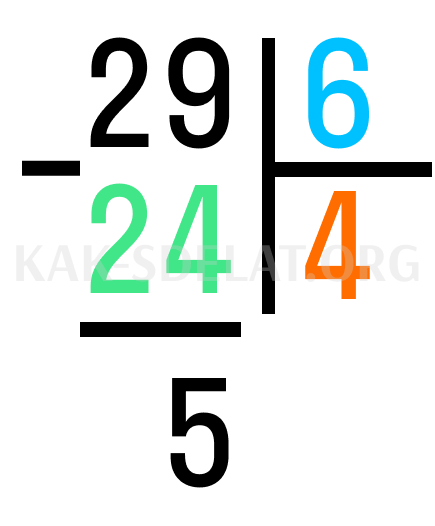
Примеры на деление в столбик для 3 класса
Применяйте свои знания на практике. Ниже мы привели несколько примеров деления двузначных и трехзначных чисел в 3 классе. Отсортируйте их по столбцам, а затем проверьте числа — без подглядывания! Обратите внимание, что на более сложном уровне существует деление многозначных чисел на двузначные, которое не рассматривается в этой статье. Это задача со звездочкой.

 lightanddesign.ru
lightanddesign.ru