Как сделать дробь с целым числом

На предыдущих уроках дроби, состоящие из целых и дробных частей, назывались смешанными числами.

Все дроби с целой и десятичной частями имеют общее название (смешанные числа).

Смешанные числа можно складывать, вычитать, умножать и делить, как и обычные дроби. В этом уроке мы рассмотрим каждую из этих функций отдельно.

Сложение целого числа и правильной дроби

Могут возникнуть проблемы, когда нужно добавить целые числа к дробям. Например, сложите 2 и дробь. Чтобы решить этот пример, представьте число 2 в виде дроби. Затем сложите дроби с разными знаменателями.

Внимательно посмотрите на этот пример. Изучите его начало и конец. Начало выглядит так, а конец — так. Разница в том, что в первом случае число 2 и дробь соединены знаком сложения, тогда как во втором случае они пишутся вместе. На самом деле это одно и то же. Важно отметить, что существуют сжатые и несжатые формы, в которых записываются смешанные числа.

Мы должны понять, что когда перед нами смешанное число форм, знак сложения опускается.

Какие выводы можно сделать? Если мы складываем целые и дробные числа, мы можем опустить знак плюс и записать целые и дробные числа вместе.

В этом случае значение уравнения будет таким

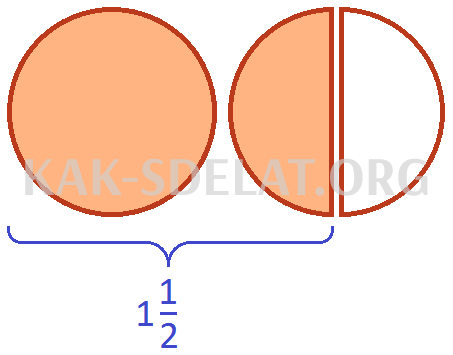
При добавлении половины пиццы к двум целым пиццам получаются две полные пиццы и половина пиццы.

Пример 2. Нахождение значения

Запишите число 3 в виде дроби. Затем сложите дроби с разными знаменателями.

Это первый метод. Второй метод намного проще. Вы можете записать целую и дробную части вместе, добавив знак равенства. Другими словами, опустите знак "плюс".

Пример 3. Нахождение значения выражения

Можно написать 2 и дробь вместе, но это не окончательный ответ, так как можно выбрать целую часть дроби.

Поэтому в данном примере сначала отделяется целая часть дроби. Доля пяти секунд — это два целых числа и доля одной секунды.

Теперь в основном выражении вместо дробей мы пишем смешанные числа

Есть новое выражение. В этом выражении смешанные числа записаны в развернутом виде.

Применим комбинаторный закон сложения. Добавьте два, чтобы получить четыре.

Затем сложите получившееся смешанное число.

Это окончательный ответ. Подробное решение этого примера можно записать следующим образом

Сложение смешанных чисел

Проблема в том, что вам нужно сложить смешанное число. Например, найдите значение выражения. Чтобы решить этот пример, сложите отдельно целую и дробную части.

Сначала смешанное число записывается в развернутом виде.

Примените комбинаторный закон сложения. Группируйте целые и десятичные части отдельно.

Вычислим целые числа: 2 + 3 =5. В основном выражении замените выражение в скобках (2 + 3) на получившуюся пятерку.

Затем вычислите десятичную часть. При этом складываются дроби с разными знаменателями. Мы уже знаем, как складывать такие дроби.

Получено Затем замените дробную часть основного выражения полученной дробью.

Затем сложим получившееся смешанное число.

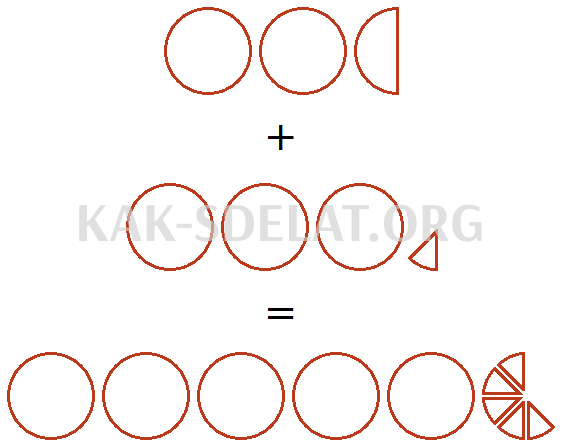
Таким образом, значение выражения равно. Представим это решение в виде графика. При сложении трех целых и одной восьмой пиццы с двумя целыми и одной половиной пиццы получается пять целых и пять восьмых пиццы.

Примеры, подобные этому, нужно решать быстро, не останавливаясь на проработке деталей. Если бы мы учились в школе, то решение этого примера следовало бы записать следующим образом

Если вы увидите такой ярлык в будущем, не паникуйте. Вы уже понимаете, откуда он берется.

Пример 2. Нахождение значения выражения

Запишите смешанное число в развернутом виде.

Сгруппируйте отдельно целые и дробные части.

Вычислите набор отрезков: 5 + 3 = 8. В основной формуле замените выражение в скобках (5 + 3) на полученное 8.

Затем вычислите дробные части.

Существует смешанное число. Теперь в основном выражении заменим выражение в скобках на смешанное число

Теперь у нас есть выражение. В данном случае нам нужно добавить число 8 к целой части смешанного числа. Для этого мы можем временно расширить смешанное число, чтобы уточнить, к чему мы прибавляем.

Добавьте целое число. Получить 9.

Минимизируйте окончательный ответ.

Следовательно, значение выражения равно.

Полное решение этого примера выглядит следующим образом

Существует универсальное правило для решения подобных примеров. Это выглядит следующим образом:.

Чтобы сложить смешанные числа:.

• Свести части этих чисел к общему знаменателю.
• Складывайте целые и дробные числа отдельно.

Если сумма дробных частей приводит к неправильной дроби, выделите целую часть этой дроби и прибавьте ее к целому числу.

Использование готовых правил допустимо, если тема полностью понятна. Решения по формулам, которые ищут другие похожие примеры, приводят к ошибкам, на поиск которых уходит дополнительное время. Поэтому предпочтительнее сначала понять предмет, а затем использовать готовые правила.

Пример 3. Нахождение значения выражения

Используйте правило готовности. Приведите дробные части к общему знаменателю и сложите отдельно целые и дробные части.

Сложение целого и смешанного числа

Некоторые задачи требуют сложения целых и смешанных чисел. Например, сложите 2 и смешанное число. В этом случае целое число прибавляется отдельно, а дробная часть остается неизменной.

Здесь смешанная фракция расширялась в процессе растворения, а затем вся часть группировалась и добавлялась. Наконец, целые и дробные части были свернуты. В результате был получен ответ.

Представим это решение в виде диаграммы. Добавьте целую пиццу и три пиццы к двум пиццам, и у вас получится целая пицца и три пиццы.

Пример 2. Нахождение значения

В этом примере добавьте целые части, как в предыдущем.

Целая и дробная части не складываются, но суть в том, что дробная часть является неправильной дробью. Сначала необходимо извлечь всю часть этой нерегулярной фракции. Затем прибавьте целую часть этой дроби к 4, оставив дробную часть без изменений. Продолжим этот пример новой строкой.

Вычитание дроби из целого числа

Существует ряд проблем, в которых необходимо удалить небольшую часть целого числа. Например, удаление части числа. Чтобы решить такой пример, представьте целое число 1 в виде дроби и отнимите дроби с разными знаменателями.

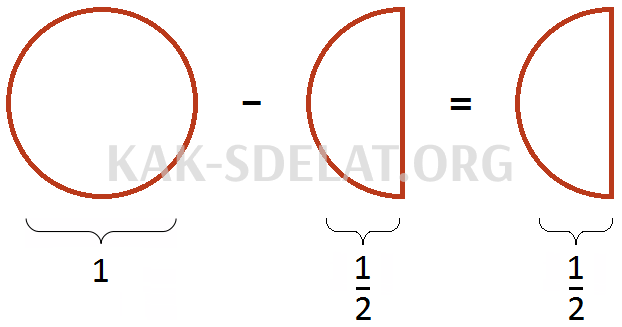
Если у нас есть целая пицца и мы удалим половину, у нас будет половина пиццы.

Пример 2. Найдите значение представления.

Представьте число в виде дроби. Извлеките дроби с разными знаменателями.

Если есть две целые пиццы и вы удалите нижнюю половину, у вас получится половина пиццы.

Эти примеры можно решить в уме. Вы можете воспроизвести их только в своем воображении. Например, найти значение выражения без необходимости вычисления тезиса.

Предположим, что число 3 — это три пиццы.

Вам нужно удалить их. Помните, что одна треть — это

Теперь представьте, как будут выглядеть три пиццы, если одну из них разрезать.

Результат (две пиццы и две трети).

Чтобы проверить правильность решения, можно использовать обычный метод для нахождения значения уравнения. Покажите значение 3 в виде дроби и вычтите дробь с другим знаменателем.

Пример 3. Нахождение значения

Число 3 дано в виде дроби. Затем вычтите дроби с разными знаменателями.

Вычитание смешанного числа из целого числа

Теперь вы готовы вычесть смешанное число из целого числа. Найдите значение числа 3.

Чтобы решить этот пример, представьте число 5 в виде дроби и преобразуйте смешанное число в неправильную дробь. После преобразования смешанного числа в неправильную дробь получите дробь. Затем вычтите дроби с разными знаменателями.

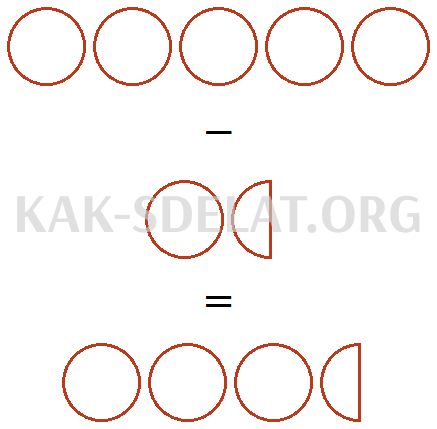
Из пяти целых пицц вычтите одну целую пиццу и половину пиццы, оставив три полные пиццы и половину пиццы.

Пример 2. Нахождение значения

6 в виде дроби и представлять смешанные числа в виде неправильных дробей. При преобразовании смешанного числа в неправильную дробь получается Затем вычтите дроби с разными знаменателями.

Примеры вычитания дробей из чисел или смешанных дробей из чисел опять же можно выполнить мысленно. Процесс легко понять.

Например, если вы хотите найти значение выражения, вам не нужно выражать 2 в виде дроби, а затем вычитать дроби с разными знаменателями. Если рассматривать вторую пиццу как две целые пиццы, то можно представить, что две трети были отрезаны.

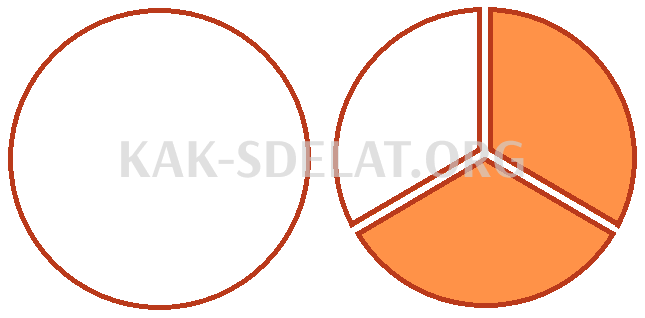
Разрезанные пиццы затем превращаются в остатки пиццы. Кроме того, одна из пицц останется нетронутой. Таким образом, получается целая пицца и одна треть пиццы.

Накройте рукой две трети пиццы на рисунке (заштриховано), и это сразу станет заметно.

Вычитание смешанных чисел

Есть несколько задач, в которых нужно вычесть из смешанного числа другое смешанное число. Например, нахождение значения выражения.

Чтобы решить этот пример, преобразуйте смешанное число в неправильную дробь, а затем вычтите дробь с другим знаменателем.

При вычитании из дроби из трех целых чисел двух целых чисел и одной третьей части пиццы остается одно целое число и одна шестая часть пиццы.

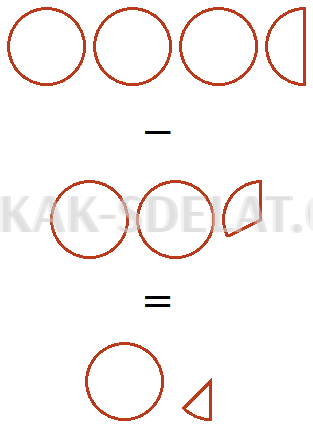
Пример 2. Нахождение значения

Преобразование смешанного числа в неправильную дробь и вычитание дробей с разными знаменателями.

Вернитесь к вычитанию смешанных чисел. В вычитании дробей есть тонкости, которые еще не готовы для начинающих. Например, числитель может быть меньше знаменателя. Это может привести нас в мир отрицательных чисел, который мы еще не изучали.

А пока давайте рассмотрим умножение смешанных чисел. К счастью, это не так сложно, как сложение и вычитание.

Умножение целого числа на дробь

Чтобы умножить целое число на дробь, умножьте целое число на дробный числитель и не меняйте знаменатель.

Например, давайте умножим число 5 на дробь. Чтобы решить этот пример, умножьте 5 на числитель и не меняйте знаменатель.

Ответ — неправильная дробь. Различать целые части дробей.

Если есть пять целых пицц и вы возьмете половину из них, у вас будет две целых пиццы и половина пиццы.

Пример 2. Нахождение значения

Умножьте 3 на числитель дроби

Ответ — неправильная дробь, но целое было удалено, чтобы получить 2.

Вы также можете сократить его. Результат будет тот же. Это будет выглядеть следующим образом

Есть три целых пиццы, и если взять две трети от этого числа, то получится две целых пиццы.

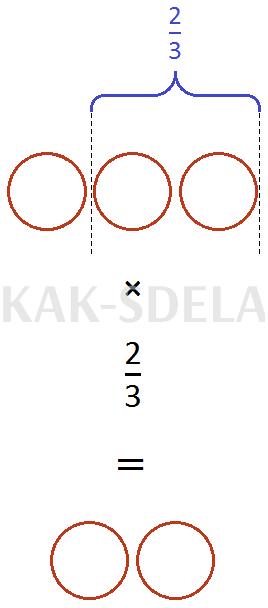
Пример 3. Нахождение значения

Этот пример решается так же, как и предыдущий. Вам нужно умножить целое число на числитель дроби.

Пример 4. Нахождение значения выражения

Умножьте 3 на числитель дроби

Умножение смешанного числа на дробь

Чтобы умножить смешанное число на дробь, преобразуйте смешанное число в неправильную дробь, а затем умножьте дробь на дробь.

Пример 1. Нахождение значения выражения

Переведите смешанное число в неправильную дробь. После перевода число превращается в дробь. Затем вы можете умножить эту дробь на

Предположим, что у нас есть целых полтора:.

Умножив эти части на коэффициент, вы получите две трети от них. Чтобы получить эти две трети, сначала разделите их на три равные части. Разделите пиццу слева на две половины. Тогда у нас будет три равных ломтика.

Если теперь мы возьмем (два из трех имеющихся), то получим целую пиццу. Для наглядности давайте заштрихуем эти два среза.

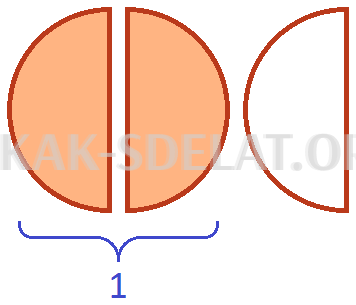
Таким образом, значение уравнения равно 1.

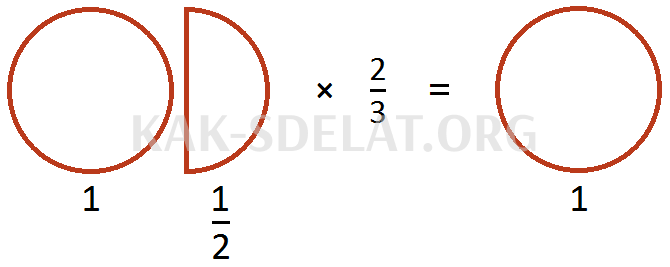
Умножение смешанных чисел

Есть несколько задач, в которых нужно перемножить смешанные числа. Например, при умножении. Чтобы решить этот пример, нужно преобразовать смешанные числа в неправильные дроби, а затем перемножить неправильные дроби.

Для понимания этого примера воспользуемся диаграммой. Предположим, у вас есть половина целой пиццы.

Теперь давайте разберемся со смешанным множителем. Этот множитель означает, что вам нужно взять всю пиццу и половину пиццы дважды и еще один раз.

Использование множителя 2 означает, что всю пиццу нужно проглотить дважды. Возьмите две целые пиццы и половину пиццы.

Однако, поскольку множитель был смешанным числом, нужно отнять от исходной целой пиццы полторы. Для этого вернитесь к исходным целой и половинке пиццы и разделите их поровну, чтобы получилось ровно по половине. Затем вы можете разделить целую пиццу на четыре части, а половину на две части, чтобы получить половинки.

Теперь вся пицца и половинки делятся поровну. Теперь вы знаете, что это за половинки. Эти половинки и есть пицца. Это хорошо видно, если расположить равные ломтики, как показано ниже.

А если рассматривать исходную целую пиццу и половину в таком порядке, как показано на этой схеме, то половина — это пицца.

Таким образом, значение уравнения становится

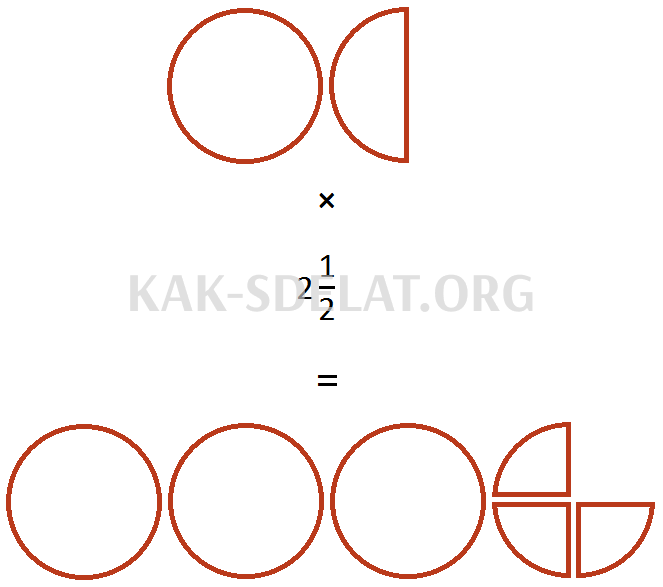
Пример 2. Нахождение значения

Преобразуйте смешанные числа в неправильные дроби и перемножьте эти неправильные дроби. Если ответ дает неправильную дробь, разделите целую дробь.

Деление целого числа на дробь

Чтобы разделить целое число на дробь, умножьте целое число на обратную величину делителя.

Например, разделите число 3 на дробь. Здесь число 3 является делителем, а дробь — делимым.

Чтобы решить этот пример, умножьте 3 на . Умножьте на обратную величину . А обратная дробь равна. Поэтому умножьте 3 на дробь.

Предположим, есть три пиццы.

Если мы зададим вопрос: "Сколько раз (половинок пиццы) в трех пиццах?", то ответ будет "шесть раз".

На самом деле, если каждую пиццу разрезать пополам, то получится шесть половинок.

Следовательно, значение уравнения равно 6.

Пример 2. Нахождение значения выражения

Чтобы решить этот пример, число 2 нужно умножить на обратную дробь. Обратная часть дроби является дробью.

Предположим, есть две целые пиццы.

Сколько пицц содержится в этих двух пиццах?". Задайте вопрос "Сколько пицц содержится в этих двух пиццах?". Чтобы ответить на этот вопрос, выделите целую часть дроби. После извлечения целой части дроби

Задайте следующий вопрос: "Сколько раз включены две пиццы (пицца и половина пиццы)?".

Чтобы ответить на этот вопрос, найдите количество пятен на двух пиццах, изображенных на следующем рисунке.

Две пиццы содержат целую пиццу и половину пиццы. Это можно понять, если вторую пиццу разделить посередине.

Вторая половина — это тогда одна треть, и она не помещается. Причина этого заключается в том, что вся пицца может быть разделена в центре. Каждый ломтик составляет треть от этого количества.

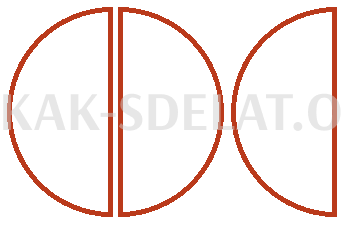
Таким образом, значение уравнения становится

Пример 3. Нахождение значения

Чтобы решить этот пример, нужно умножить число 5 на обратную дробь. Обратной дробью является дробь. Поэтому умножьте 5 на 5.

Дробь — это два целых числа. Проще говоря, поставьте два целых числа и четверть дроби.

Затем выражение определяет, сколько раз будет пять пицц. Ответ — смешанное число.

Это означает, что пицца содержится в пяти пиццах.

Найдите удвоенное количество пицц в пяти пиццах.

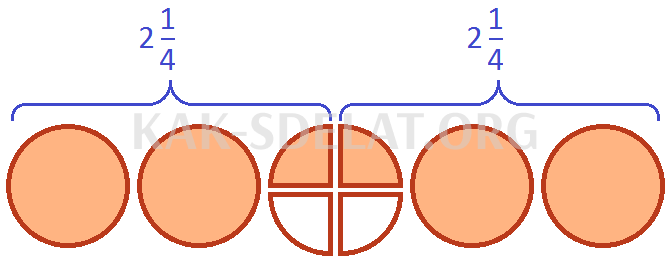
Осталось две четверти белого цвета. Эти две четвертинки взялись и не подошли. Причина этого в том, что две девятки можно разделить на четыре части всей пиццы. Тогда каждый ломтик составляет одну девятую от этого количества, а два ломтика — два из девяти.

Таким образом, значение уравнения становится

Деление дроби на целое число

Чтобы разделить дробь на целые числа, эту пропорцию нужно умножить на обратную величину делителя. Мы создали это деление в одном из предыдущих уроков. Вспомните еще раз.

Пример 1. Деление дроби на 2.

Чтобы разделить дробь на два, умножьте обратное двум число на 2. Обратное число 2 равно

Предположим, у нас есть половина пиццы:.

Разделите его на две части. Тогда каждая возникшая дробь будет равна четверти пиццы.

Таким образом, значение уравнения становится

Пример 2. Нахождение значения выражения

Чтобы решить этот пример, нужно умножить обратное 2 на обратное 2.

Пример 3. Нахождение значения

Умножьте первую дробь на обратное число 3. Обратное число 3 — это дробь.

Деление целого числа на смешанное число

Вы можете захотеть разделить целое число на смешанное число. Например, разделите 2.

Чтобы решить этот пример, измените делитель на неправильную дробь. Затем умножьте обратную дробь делителя на 2.

Изменяя делитель на неправильную дробь, получаем Далее мы умножаем 2 на обратную дробную ставку. Обратная дробь.

Предположим, есть две целые пиццы.

Задайте вопрос: "Сколько раз (целая и половинка пиццы) входит в две пиццы?". . Похожий пример мы решали ранее, когда учились делить целые числа на дроби.

Две пиццы содержат целую пиццу и половину пиццы. Это можно понять, если вторую пиццу разделить посередине.

Вторая половина — это тогда одна треть, и она не помещается. Причина этого заключается в том, что вся пицца может быть разделена в центре. Каждый ломтик составляет треть от этого количества.

Таким образом, значение уравнения становится

Пример 2. Нахождение значения

Измените делитель на неправильную пропорцию. Затем умножьте дробь, которая является обратной пропорцией, на 5. Это обратная величина по отношению к дроби

Получив первоначальный ответ, мы уменьшили эту дробь на 5. Мы получили, но не были удовлетворены и этим ответом, так как это была неправильная дробь. Эта неравномерная дробная часть была разделена на целые числа. В результате был получен ответ

Деление смешанного числа на целое число

Чтобы разделить смешанное число на целое число, преобразуйте смешанное число в неправильную дробь и умножьте дробь на обратную величину делителя.

Например, чтобы решить этот пример, преобразуйте делитель в неправильную дробь. Затем умножьте эту дробь на число, обратное делителю 2.

Преобразуйте смешанное число в неправильную дробь и получите.

Затем умножьте это число на число, обратное 2. Обратное число 2 — это

Предположим, у нас есть половина пиццы:.

Давайте разделим это число на две равные части. Сначала разделите всю пиццу на две части.

Затем разделите его на две равные части и разделите пополам.

Теперь разделите эти кусочки на две группы, у каждой группы есть пицца.

Следовательно, значение выражения равно

Пример 2. Нахождение значения

Измените делитель на неправильную пропорцию. Затем умножьте на его обратную величину 4. Обратной величиной 4 является исис.

Деление смешанных чисел

Чтобы разделить смешанное число, преобразуйте число в неправильную дробь, а затем создайте деление на обычный фрагмент. То есть, умножьте первую дробь на обратную часть второй дроби.

Пример 1. Нахождение значения выражения

Преобразуйте смешанное число в неправильную дробь. Получаем следующее уравнение.

Мы уже знаем, как решить эту проблему. Умножьте первую дробь на обратную часть второй дроби. Обратная часть второй дроби.

Решите этот пример до конца.

Предположим, у нас есть два целых числа и одна половина дроби.

Если мы зададим вопрос: "Сколько раз (целых и четвертных) входит в две пиццы и одну половинку?", то ответ будет "два раза".

Пример 2. Нахождение значения

Преобразуйте смешанное число в неправильную дробь. Получаем следующее уравнение.

Затем умножьте первую дробь на обратную часть второй дроби. Обратный показатель дроби.

Сначала получите фракцию. Мы уменьшили эту фракцию на 9. В результате мы получили дроби, но такой ответ нас не устроил, и мы разделили целую часть дроби на дробь. В результате был получен окончательный ответ.